Kalkulačka s pevným povrchem |
| a = | |
| r = | |
| Units: | |
| Surface Area = | 0 |
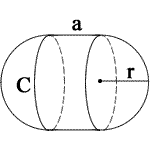 a = side length
a = side lengthr = radius
Povrchová plocha kruhového kužele
- .
Laterální povrchová plocha = πrs = πr√ (r 2 + h 2 )
Základní plocha povrchu = πr 2
Celková plocha povrchu
= L + b = πrs + πr 2 = πr (s + r) = πr (r + √ (r 2 + h 2 ) )
Plocha povrchu kapslí
- .
Povrchová plocha = 2πR (2R + A)
Plocha kruhového válce
- .
Horní plocha povrchu = πr 2
Spodní povrchová plocha = πr 2
Celková plocha povrchu
= L + t + b = 2πRH + 2 (πr 2 ) = 2πr (h + r)
Povrchová oblast kostka
- .
Povrchová plocha = 6a 2
Kuželová plocha
- .
Laterální povrchová plocha
= π (r 1 + r 2 ) s = π (r 1 + r 2 ) √ (((( r 1 - r 2 ) 2 + h 2 )
Horní plocha povrchu = πr 1 2
Základní plocha povrchu = πr 2 2
Celková plocha povrchu
= π (r 1 2 + r 2 2 + (r 1 * r 2 ) * s)
= π [r 1 2 + r 2 2 + (r 1 * r 2 ) * √ ((r 1 - r 2 ) 2 + h 2 )]
Povrchová plocha polokoule
- .
Zakřivená plocha povrchu = 2πr 2
Základní plocha povrchu = πr 2
Celková plocha povrchu = (2πr 2 ) + (πr 2 ) = 3πr 2
Obdélníkový hranolový povrch
- .
Povrchová plocha = 2 (LW + LH + WH)
Pyramidová plocha
- .
Laterální povrchová plocha = A√ (a 2 + 4h 2 )
Základní plocha povrchu = 2
Celková plocha povrchu
= L + b = a 2 + a√ (a 2 + 4h 2 ))
= A (A + √ (A 2 + 4h 2 ))
Plocha sférické plochy
- .
Povrchová plocha = 2πRH
Plocha povrchu koule
- povrchová plocha = 4πr 2
Například k sféře, když R = 3
- .
Pro výpočet povrchové plochy koule použijte následující vzorec: 4πr 2 . Při nahrazení R pro svou hodnotu získáte 4π * 3 2 , což se rovná 113.09734 m 2 .
Například k kužele, když R = 3, H = 3
- .
Pro výpočet povrchové plochy kužele použijte následující vzorec: πr (r + √ (r 2 + h 2 )). Když nahradíte R a H pro jejich hodnoty, získáte π3 (3 + * radik; (3 2 + 3 2 ), což se rovná 68.26028 m 2 .
výběr jazyka:日本語 | 한국어 | Français | Español | ไทย| عربي | русский язык | Português | Deutsch| Italiano | Ελληνικά | Nederlands | Polskie| Tiếng Việt| বাংলা| Indonesia| Pilipino| Türk| فارسی| ລາວ| ဗမာ| български| Català| čeština| Қазақ| Magyar| Română| Україна
Copyright ©2021 - 2031 All Rights Reserved.