Anrulus kalkulačka

r₁ =
r₂ =
Units:

C₁ =	0
C₂ =	0
A₁ =	0
A₂ =	0
A₀ =	0

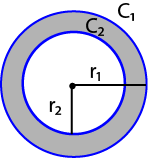
annulus

R _{1 = vnější poloměr}

r _{2 = vnitřní poloměr}

C _{1 = vnější obvod}

C _{2 = vnitřní obvod}

A _{1 = oblast kruhu r ₁}

A _{2 = oblast kruhu r ₂}

A _{0 = stínovaná oblast}

Online anuluje kalkulačku najít oblast, obvod a poloměr prstence. Když znáte dvě známá proměnná, pak vyberte z Droplistu, vypočítejte další 5 neznámé.

Anrulus vzorce:

Vzhledem k r _{1 a r _{2 :}}

C _{1 = 2πr ₁}

C _{2 = 2πr ₂}

A _{1 = πr _{1 ²}}

A _{2 = πr _{2 ²}}

A _{0 = A _{1 - A _{2 .}}}

Vzhledem k r _{1 a c _{2 :}}

r _{2 = c _{2 / 2π}}

C _{1 = 2πr ₁}

A _{1 = πr _{1 ²}}

A _{2 = πr _{2 ²}}

A _{0 = A _{1 - A _{2 .}}}

dána r _{1 a _{2 :}}

r _{2 = √ (A _{2 / π)}}

C _{1 = 2πr ₁}

C _{1 = 2πr ₂}

A _{1 = πr _{1 ²}}

A _{0 = A _{1 - A _{2 .}}}

Vzhledem k r _{2 a c _{1 :}}

r _{1 = c _{1 / 2π}}

C _{2 = 2πr ₂}

A _{1 = πr _{1 ²}}

A _{2 = πr _{2 ²}}

A _{0 = A _{1 - A _{2 .}}}

Dáno C _{1 a c _{2 :}}

r _{1 = c _{1 / 2π}}

r _{2 = c _{1 / 2π}}

A _{1 = πr _{1 ²}}

A _{2 = πr _{2 ²}}

A _{0 = A _{1 - A _{2 . Dáno c _{1 a _{2 < / sub> :}}}}}

r _{1 = c _{1 / 2π}}

r _{2 = √ (A _{2 / π)}}

C _{2 = 2πr ₂}

A _{1 = πr _{1 ²}}

A _{0 = A _{1 - A _{2 .}}}

Vzhledem k r _{2 a _{1 :}}

r _{1 = √ (A _{1 / π)}}

C _{1 = 2πr ₁}

C _{2 = 2πr ₂}

A _{2 = πr _{2 ²}}

A _{0 = A _{1 - A _{2 .}}}

Vzhledem k c _{2 a _{1 :}}

r _{1 = √ (A _{1 / π)}}

r _{2 = c _{2 / 2π}}

C _{1 = 2πr ₁}

A _{2 = πr _{2 ²}}

A _{0 = A _{1 - A _{2 .}}}

Vzhledem k _{1 a _{2 :}}

r _{1 = √ (A _{1 / π)}}

r _{2 = √ (A _{2 / π)}}

C _{1 = 2πr ₁}

C _{2 = 2πr ₂}

A _{0 = A _{1 - A _{2 .}}}

Dáno r _{1 a _{0 :}}

C _{1 = 2πr ₁}

A _{1 = πr _{1 ²}}

A _{2 = A _{1 - A ₀}}

r _{2 = √ (A _{2 / π)}}

C _{2 = 2πr _{2 .}}

Vzhledem k r _{2 a _{0 :}}

C _{2 = 2πr ₂}

A _{2 = πr _{2 ²}}

A _{1 = A _{0 + A ₂}}

r _{1 = √ (A _{1 / π)}}

C _{1 = 2πr _{2 .}}

Vzhledem k c _{1 a _{0 :}}

r _{1 = c _{1 / 2π}}

A _{1 = πr _{1 ²}}

A _{2 = A _{1 - A ₀}}

r _{2 = √ (A _{2 / π)}}

C _{2 = 2πr _{2 .}}

Vzhledem k c _{2 a _{0 :}}

r _{2 = c _{2 / 2π}}

A _{2 = πr _{2 ²}}

A _{1 = A _{0 + A ₂}}

r _{1 = √ (A _{1 / π)}}

C _{1 = 2πr _{1 .}}

Vzhledem k _{1 a _{0 :}}

A _{2 = A _{1 - A ₀}}

r _{1 = √ (A _{1 / π)}}

r _{2 = √ (A _{2 / π)}}

C _{1 = 2πr ₁}

C _{2 = 2πr _{2 .}}

Vzhledem k _{2 a _{0 :}}

A _{1 = A _{0 + A ₂}}

r _{1 = √ (A _{1 / π)}}

r _{2 = √ (A _{2 / π)}}

C _{1 = 2πr ₁}

C _{2 = 2πr _{2 .}}

Anrulus kalkulačka

FoxCalculators - Kalkulačky zdarma online!

Anrulus kalkulačka

Anrulus vzorce: