Standardní odchylka kalkulačka

Enter Inputs	5,20,40,80,100 Enter the Numbers with Comma separated(,)

Result:
No.of Inputs
Mean
Standard Deviation(SD)
Population Standard Deviation(PSD)
Variance(SD)
Variance(PSD)
Calculation

Standardní odchylka kalkulačka pro výpočet společného měření šíření datové sady je to analýza dat. Kalkulačka by vám mohla dát no.of vstupy, střední, standardní odchylku (SD), standardní odchylku populace (PSD), rozptyl (SD), rozptyl (PSD) daných vstupních hodnot datové sady.

Standardní odchylka vzorec

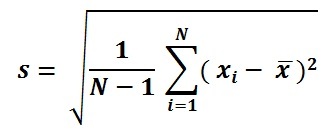
Standard Deviation Formula & Calculation

Obyvatelstvo SD Formula.

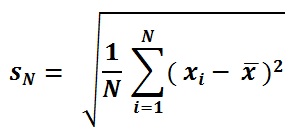
PSD - Population Standard Deviation Formula & Calculation

Rozptylu vzorec

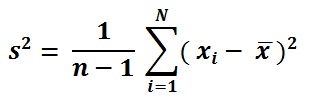
Variance Formula & Calculation

Střední vzorec

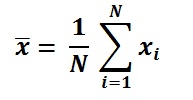
Mean Formula & Calculation

Například, když se dáte sada dat 5,20,40,80,100 , výsledek bude:

.

Celkové vstupy (n) = (5,20,40,80,100)

Celkové vstupy (n) = 5

Střední (xm) = (x1 + x2 + x3 ... xn) / n

Průměr (xm) = 245/5

Prostředky (xm) = 49

-------------------------------------------

SD =

SQRT (1 / (n-1) * ((x1-xm) ^ 2 + (x2-xm) ^ 2 + .. + (xn-xm) ^ 2))

= SQRT (1 / (5-1) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2 + (100-49) ^ 2 ))

= SQRT (1/4 ((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRT (1/4 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1605)

= 40.0625.

Variance = SD ^ 2

Variance = 40.0625 ^ 2

Variance = 1605.

-------------------------------------------

PSD =

SQRT (1 / (n) * ((x1-xm) ^ 2 + (x2-xm) ^ 2 + .. + (xn-xm) ^ 2))

= SQRT (1 / (5) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2 + (100-49) ^ 2))

= SQRT (1/5 ((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRT (1/5 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1284)

= 35.8329.

Variance = SD ^ 2

Variance = 35.8329 ^ 2

Rozptyl = 1284.

Standardní odchylka kalkulačka

FoxCalculators - Kalkulačky zdarma online!